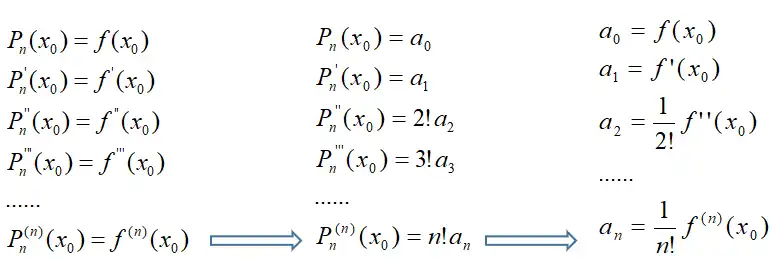中值定理
我们可以这样写:
f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0)
因为 f′(x0)=limx→x0x−x0f(x)−f(x0),所以上式成立。而 o(x−x0) 是无穷小量,所以 f(x)≈f(x0)+f′(x0)(x−x0)。
从几何上看,它是用切线近似代替曲线。然而,这样的近似是比较粗糙的,而且只在点的附近才有近似意义。为了改善上述不足,使得近似替代更加精密,数学家们在柯西中值定理的基础上,推导出了泰勒中值定理(泰勒公式)。
推导过程
给定一个函数 f(x),要找一个在指定点 x0 附近与 f(x) 很近似的多项式函数 P(x),记为:
Pn(x)=a0+a1(x−x0)+a2(x−x0)2+⋯+an(x−x0)n
使得 f(x)≈Pn(x) 可估计。那么,该多项式要满足什么条件,误差又是什么?
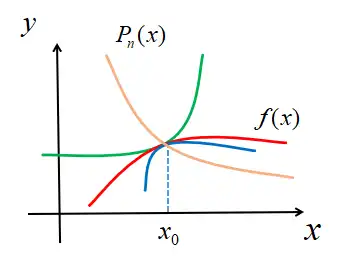
从几何上看,y=f(x),y=Pn(x) 代表两条曲线,如下图:

使它们在 x0 附近很靠近,很明显:
- 首先要求两曲线在点 (x0,f(x0)) 相交,即 Pn(x0)=f(x0);
- 如果要靠得更近,还要求两曲线在点 (x0,f(x0)) 相切(由图像可以直观看出,相交:橙色 和 红色 图像;相切:绿色 和 红色 图像,两曲线在 x0 附近的靠近情况明显差异很大,相切更近),即 Pn′(x0)=f′(x0);
- 如果还要靠得更近,还要求曲线在点 (x0,f(x0)) 弯曲方向相同(如上图,弯曲方向相反:绿色 和 红色 图像;弯曲方向相同:蓝色 和 红色 图像,明显在离 x0 很远的地方,弯曲方向相同两函数的差异更小一点),即 Pn′′(x0)=f′′(x0),进而可猜想,若在 (x0,f(x0)) 附近有 Pn′(x0)=f′(x0),Pn′′(x0)=f′′(x0),……,Pn(n)(x0)=f(n)(x0),近似程度越来越好。
综上所述,所要找的多项式应满足下列条件:

如何得出结论的呢?以上图三行二阶导数为例:
- 第一个箭头:将 Pn(x) 求二阶导后代入 x0,求得 Pn′′(x0)=2!a2。
- 第二个箭头:所以 f′′(x0)=2!a2,所以 a2=2!1f′′(x0),多项式函数:
Pn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n
其中系数 a 可全用 f(x) 表示,得:
Pn(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+…+n!f(n)(x0)(x−x0)n
其中误差 Rn(x)=f(x)−Pn(x)。因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一些误差。
这样,我们就得到了泰勒公式的定义:
如果函数 f(x) 在含 x0 的某个开区间 (a,b) 内具有直到 (n+1) 阶导数,则对 ∀x∈(a,b),有:
f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+…+n!f(n)(x0)(x−x0)n+Rn(x)
其中余项(即误差):
Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1
ξ 在 x0 与 x 之间。这种余项表达方式称为 n 阶泰勒展开式的拉格朗日余项。拉格朗日余项是 n 阶泰勒公式又多展开了一阶,n 变为 n+1。
麦克劳林公式
这是泰勒公式的一种特殊情况:即当 x0=0 时的泰勒公式。所以将 x0=0 带入公式,即得:
f(x)=0!f(0)+1!f′(0)x+2!f′′(0)x2+…+n!f(n)(0)xn+Rn(x)
几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:
- ex=1+x+2!1x2+…+n!1xn+o(xn)
- sinx=x−3!1x3+…+(2m−1)!(−1)m−1x2m−1+o(x2m−1)
- cosx=1−2!1x2+4!1x4−…+(2m)!(−1)mx2m+o(x2m)
- ln(1+x)=x−21x2+31x3−…+n(−1)n−1xn+o(xn)
佩亚诺余项为 (x−x0)n 的高阶无穷小:Rn(x)=o[(x−x0)n]。